这个学期报了学校开设的计算机图形学课程，由于前一个月老师讲的都太抽象完全不知道在说啥……于是我的入门现在才刚刚开始。最近的一节课教授了基本图元的生成算法，留的作业是使用OpenGL或者DirectX实现DDA算法画直线、方程法画圆以及Bresenham画直线和圆。

ps：本次作业使用的是OpenGL中的<GL/glut.h>库

对于窗口的配置

原本默认的窗口是左下角坐标是(-1, -1)，右上角坐标为(1, 1)，窗口的中心坐标为(0, 0)。在此绘制的是1000*600的窗口，左下角坐标为(0, 0)，右上角坐标为(1000, 600)。且变换窗口大小图形的大小和位置不会改变。这一操作中起到关键作用的函数是gluOrtho2D和glViewport，具体的理解可以参考这里：gluOrtho2D、glViewport、glutInitWindowSize区别与关系

大致的窗口配置如下：

cpp

void Init()
{
    glClearColor(1.0, 1.0, 1.0, 1.0);
    glMatrixMode(GL_PROJECTION);
    glLoadIdentity();
    gluOrtho2D(0, 1000, 0, 600);
}

int main(int argc, char** argv)
{
    glutInit(&argc, argv);
    glutInitDisplayMode(GLUT_RGB | GLUT_SINGLE);
    glutInitWindowPosition(500, 250);
    glutInitWindowSize(1000, 600);
    glutCreateWindow("MyDraw");
    Init();
    glutDisplayFunc(display);
    glutMainloop();
}

DDA算法绘制直线

DDA算法的原理很简单，即求出用户输入直线两端的坐标 $(x 1, y 1), (x 2, y 2)$ 后求出要绘制直线的斜率 $k$ 。然后先画出更靠左的点，接着依次绘制 $(x_{i} + 1, r o u n d (y_{i} + k))$ ，直到最右边的点即可。

在算法的实现过程中容易注意不到的错误有三个：

在斜率绝对值大于1时，再以x为步长每次自增1，会导致直线变成由离散的点组成的虚线。此时应该交换x和y的地位再进行绘图。
忽略 x1=x2 的情况，计算斜率时分母为零（但是画出的结果依然是正确的……）。
由于画直线默认是从左向右画，但是假如先输入的坐标更靠右，即x1>x2，需要调换两点坐标，否则无法画出直线。

实现的display函数如下：

cpp

void MyDraw::DDA_Draw()
{
    glClear(GL_COLOR_BUFFER_BIT);
    glViewport(0, 0, 1000, 600);
    glColor3f(0, 0, 0);

    if(x1 == x2) {  // 对于横坐标相等的点的特殊处理
        if(y1 > y2) swap(y1, y2);
        glBegin(GL_POINTS);

        for(double y = y1; y<=y2; y++)
            glVertex2f(x1, y);

        glEnd();
        glFlush();
        return;
    }
    else if(x1 > x2) {  // 保证先绘制的是更靠左的点
        swap(x1, x2);
        swap(y1, y2);
    }

    double k = (y2-y1)/(x2-x1);	// 计算出斜率k

	glBegin(GL_POINTS);

    if(fabs(k) <=1) {
        for(double x=x1, y=y1; x<=x2; x++, y+=k)
            glVertex2f(x, round(y));
    }
    else {  // 当斜率绝对值大于1时，交换原本x和y的地位进行计算
        double xStep = 1/k;
        if(k > 0)
            for(double x=x1, y=y1; y<=y2; y++, x+=xStep)
                glVertex2f(round(x), y);
        else
            for(double x=x1, y=y1; y>=y2; y--, x-=xStep)
                glVertex2f(round(x), y);
    }

    glEnd();

    glFlush();
}

DDA算法容易实现，非常直观，但是缺点也很明显，因为涉及了太多次浮点运算，所以不利于硬件实现，并不实用。

Bresenham算法绘制直线

以下关于算法的叙述适用于斜率 $k$ 位于0和1之间的情况下。

在绘出点 $(x_{i}, y_{i})$ 后，要确定 $(x_{I + 1}, y_{i + 1})$ 的位置，实际上就是确定 $(x_{i + 1}, y_{i + 1})$ 是在下一个网格线段中点的上方还是下方，如图：

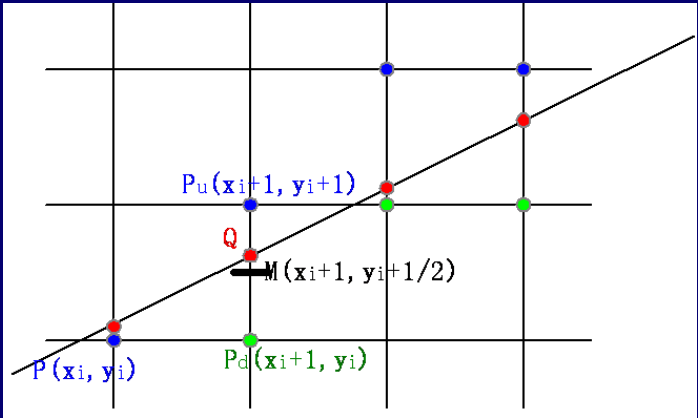
对于判断直线点在直线上还是在直线下，利用直线方程可以很容易地做到，即对于直线 $y = k x + b$ ，可以令函数 $F (x, y) = y - k x - b$ ，对于点 $(x, y)$ ：

对于直线上的点， $F (x, y) = 0$ ；
对于直线上方的点， $F (x, y) > 0$ ；
对于直线下方的点， $F (x, y) < 0$

选定一个判别变量d，有 $d_{i} = F (x_{i} + 1, y_{i} + 0.5) = y_{i} + 0.5 - k (x_{i} + 1) - b$

则有

y_{i + 1} = {\begin{cases} y_{i} + 1 (d_{i} < 0) \\ y_{i} (d_{i} \geq 0) \end{cases}

当 $d_{i} \geq 0$ 时， $d_{i + 1} = F (x_{i} + 2, y_{i} + 0.5) = d_{i} - k$

当 $d_{i} < 0$ 时， $d_{i + 1} = F (x_{i} + 2, y_{i + 1.5}) = d_{i} + 1 - k$

且 $d_{0} = F (x_{0} + 1, y_{0} + 0.5) = 0.5 - k$

由上可知绘制过程即为绘制像素点和继续对下一个d的值的判断。当时上述的算法并没有摆脱浮点运算，所以改进版使用 $2 d Δ x$ 代替 $d$ ，如下：

输入直线的两端点 $P_{0} (x_{0}, y_{0})$ 和 $P_{1} (x_{1}, y_{1})$ 。
计算初始值 $Δ x, Δ y, d = Δ x - 2 Δ y, x = x_{0}, y = y_{0}$ 。
绘制点 $(x, y)$ 。判断 $d$ 的符号。若 $d < 0$ ，则 $(x, y)$ 更新为 $(x + 1, y + 1)$ ， $d$ 更新为 $d + 2 Δ x - 2 Δ y$ ；否则 $(x, y)$ 更新为 $(x + 1, y)$ , $d$ 更新为 $d - 2 Δ y$ 。
当直线没有画完时，重复步骤3。否则结束。

改进后的算法很巧妙地避免了进行浮点数运算。编写代码时需要注意的点和DDA算法中一致。

display函数如下

cpp

void MyDraw::Bresenham_Draw()
{
    glClear(GL_COLOR_BUFFER_BIT);
    glViewport(0, 0, 1000, 600);
    glColor3f(0, 0, 0);

    if(x1 == x2 && y1 == y2) {
        glBegin(GL_POINTS);
        glVertex2f(x1, y1);
        glEnd();
        glFlush();
        return ;
    }

    if(x1 > x2) {   // 保证先绘制的是更靠左的点
        swap(x1, x2);
        swap(y1, y2);
    }

    int dx = abs(x2 - x1),
        dy = abs(y2 - y1),
        d, mark;
    bool flag;  // flag用于标记斜率绝对值是否大于1
    if (dx >= dy) { // k的绝对值在0和1之间时
        flag = false;
        mark = dx;
    }
    else {  // k的绝对值大于1时,交换dx，dy
        swap(x1, y1);
        swap(x2, y2);
        swap(dx, dy);
        flag = true;
        mark = dx;
    }
    d = dx - 2 * dy;
    int x = x1, xStep = x2 > x1 ? 1:-1,
        y = y1, yStep = y2 > y1 ? 1:-1;

    glBegin(GL_POINTS);

    for (int i = 1; i <= mark; i++) { // 以步长大的为基准画线
        if(!flag) glVertex2f(x, y);
        else glVertex2f(y, x);
        x += xStep;
        if (d >= 0) {
            d -= 2 * dy;
        }
        else {
            y += yStep;
            d += 2 * (dx - dy);
        }
    }

    glEnd();
    glFlush();
}

使用方程绘制圆形

使用八分法绘制圆形，利用圆很好的对称特性，只需要画出 $(\frac{π}{2}, π)$ 区间上的八分之一圆弧，即可绘制出整个圆形。

利用圆形的方程 $x^{2} + y^{2} = R^{2}$ 可以得到绘制圆形的递推公式：

x_{i + 1} = x_{i} + 1 x \subset [0, R / \sqrt{2}]

y_{i + 1} = r o u n d (\sqrt{R^{2} - x_{i + 1}^{2}})

display函数如下

cpp

void MyDraw::DiscreteDrawCircle()
{
    glClear(GL_COLOR_BUFFER_BIT);
    glViewport(0, 0, 1000, 600);
    glColor3f(0, 0, 0);

    int x, y;
    double mark =r/sqrt(2);   // 提前计算好判断时使用频繁的变量

    // glPointSize(10);
    glBegin(GL_POINTS);

    // 利用轴对称的特性，使用八分法作出圆形
    for(x = x1, y = y1 + r; x <= x1 + mark; x++) {  // 以x的变化为步长
        glVertex2f(x ,y);
        glVertex2f(x, 2*y1 - y);    // 关于y轴对称
        glVertex2f(2*x1 - x, y);    // 关于x轴对称
        glVertex2f(2*x1 - x, 2*y1 - y); // 关于原点对称

        int xx = x1 + y - y1, yy = y1 + x - x1; // (x, y)关于与坐标轴夹角为45°的直线的对称点
        glVertex2f(xx ,yy);
        glVertex2f(xx, 2*y1 - yy);    // 关于y轴对称
        glVertex2f(2*x1 - xx, yy);    // 关于x轴对称
        glVertex2f(2*x1 - xx, 2*y1 - yy); // 关于原点对称

        y = y1 + round(sqrt(r*r-(x-x1)*(x-x1)));
    }

    glEnd();
    glFlush();
}

这种算法的特点和DDA算法接近，都很简单直观易实现，但是运算量有点劝退。

ps：也可以使用极坐标方程实现方程法绘制圆形~

使用Bresenham算法绘制圆形

该算法的思想和Bresenham算法画直线一样，只是方程改成了圆形方程 $F (x, y) = x^{2} + y^{2} - R^{2}$

使用 $d - 0.25$ 代替 $d$ 优化之后同样摆脱了浮点运算：

输入圆的半径R
计算初始值 $d = 1 - R, x = 0, y = R$
绘制点 $(x, y)$ 及其在八分圆中的另外七个对称点
判断 $d$ 的符号。若 $d \leq 0$ ，则先将 $d$ 更新为 $d + 2 x + 3$ ，再将 $(x, y)$ 更新为 $(x + 1, y)$ ；否则先将 $d$ 更新为 $d + 2 (x - y) + 5$ ，再将 $(x, y)$ 更新为 $(x + 1, y - 1)$
当 $x < y$ 时，重复步骤3和4。否则结束

绘图函数如下：

cpp

void MyDraw::BresenhamDrawCircle()
{
    glClear(GL_COLOR_BUFFER_BIT);
    glViewport(0, 0, 1000, 600);
    glColor3f(0, 0, 0);

    int d = 1 - r;

    glBegin(GL_POINTS);

    for(int x= x1, y = y1 + r; x-x1 < y-y1; x++) {
        glVertex2f(x, y);
        glVertex2f(x, 2*y1 - y);    // 关于y轴对称
        glVertex2f(2*x1 - x, y);    // 关于x轴对称
        glVertex2f(2*x1 - x, 2*y1 - y); // 关于原点对称

        int xx = x1 + y - y1, yy = y1 + x - x1; // (x, y)关于与坐标轴夹角为45°的直线的对称点
        glVertex2f(xx ,yy);
        glVertex2f(xx, 2*y1 - yy);    // 关于y轴对称
        glVertex2f(2*x1 - xx, yy);    // 关于x轴对称
        glVertex2f(2*x1 - xx, 2*y1 - yy); // 关于原点对称

        if(d <= 0) {
            d += 2*(x-x1) +3;
        }
        else {
            d += 2*((x-x1)-(y-y1)) + 5;
            y--;
        }
    }

    glEnd();
    glFlush();
}

成果的展示就是一个圈圈……

关于使用类来综合几个display函数

glutDisplayFunc函数的参数是一个没有参数的函数指针，也就是说，起到绘制图形作用的display函数是不允许有参数的。但是这项作业还要求输入坐标绘制图形，感觉使用全局变量不是一个很好的行为（而且全局变量还不允许定义y1……），本着面(shi)对(li)对(cai)象(ji)的思想，我感觉用class来综合这些东西比较合适。让输入的坐标值都作为class中的私有变量，既可以避免使用全局变量，也让整个程序会变得好看很多。

但是这个OpenGL是一个C API，然后在glutDisplayFunc中调用类中的函数时，因为无法识别类中的this指针，所以会报一个这样的错误：

error: invalid use of non-static member function ‘void MyDraw::DDA_Draw()’ glutDisplayFunc(p.DDA_Draw);

上网查了一下资料(比如这里和这里)，发现我的原来的想法有点过于美好了。然后改进的方式是把绘图函数和表示坐标的数字改成static的。C++中的static变量和函数和Java里好像差别不小的样子？反正我的初始化最后变成了这个样子：

cpp

class MyDraw {
public:
    MyDraw();
    void InputInformationOfLine();
    void InputInformationOfCircle();
    static void DDA_Draw();
    static void Bresenham_Draw();
    static void DiscreteDrawCircle();
    static void BresenhamDrawCircle();
private:
    static double x1, y1, x2, y2, r;
};

MyDraw::MyDraw() {}

double MyDraw::x1 = 0, MyDraw::y1 = 0, MyDraw::x2 = 0, MyDraw::y2 = 0, MyDraw::r = 0;

勉强能用。

~~ps：虽然变得更丑了~~

Glut 绘制直线和圆

对于窗口的配置 ​

DDA算法绘制直线 ​

Bresenham算法绘制直线 ​

使用方程绘制圆形 ​

使用Bresenham算法绘制圆形 ​

关于使用类来综合几个display函数 ​